Understanding how computation works part 2-1

On this post, I will try to make you understand more about computer science. So, in this part of the post we are going to see what is a automata, the different kinds that exists and how the work.. First of all, what is a finite automaton? A finite automaton is a simplified model of a computer that throws out all computer features(RAM, SSD) in exchange for being easy to understand, easy to implement in hardware and software.
A finite automaton has no permanent storage and virtually no RAM, It’s a little machine with a handful of possible states and the ability to keep track of which one of those states it’s currently in. Instead of a CPU for executing arbitrary programs, each finite automaton has a hardcoded collections of rules that determine the movements that the automaton should do in a specific situation. It starts at a state called start state, and starts to change this state when it reads character, the will follow the rules of each character.
We have a special state called “accept state”. this state will suggest if the machine is accepting or rejecting a certain sequence of inputs. With this special state we gave a machine that reads a sequence of characters and provide a yes/no output that indicates if the sequence is acceptable or not. There is a kind of automata called “deterministic”, for those one we have to respect two constraints:
- No contradictions: there are no states where the machine’s next move is ambiguous because of conflicting rules.
- No omissions: there are no states where the machine’s next move is unknown because of a missing rule.
Automatas that follows does constraints are called DFA(Deterministic Finite Automaton). Let’s try to implement a DFA in Ruby, we are going to start by the rules and the rulebook.
class FARule < Struct.new(:state, :character, :next_state)
def applies_to?(state, character)
self.state == state && self.character == character
end
def follow
next_state
end
def inspect
"#<FARule #{state.inspect} --#{character}--> #{next_state.inspect}>"
end
end
class DFARulebook < Struct.new(:rules)
def next_state(state, character)
rule_for(state, character).follow
end
def rule_for(state, character)
rules.detect { |rule| rule.applies_to?(state, character) }
end
end
Now, we have a simple API, we have #applies_to? that returns true of false to indicate if that rules applies to the particular situation, and we have #follow that returns the move that the machine should do. Now that we have the rulebook, we can build DFA object, that will report for us when the current state it’s currently in an accept state or not:
class DFA < Struct.new(:current_state, :accept_states, :rulebook)
def accepting?
accept_states.include?(current_state)
end
def read_character(character)
self.current_state = rulebook.next_state(current_state, character)
end
def read_string(string)
string.chars.each do |character|
read_character(character)
end
end
end
In the DFA object, we have 2 methods to read characters, one is #read_character that will read a single character and then will make the move according to the rules, and the other method is #read_string, that will read a string with characters, will read each character and then it will make the move for each character. To avoid doing the whole wrap up of a DFA manually, we will implement an object called “DFADesign”, this object will provide us a design of a particular DFA and we will build the DFA instance with this object, and also check the acceptance of a string:
class DFADesign < Struct.new(:start_state, :accept_states, :rulebook)
def to_dfa
DFA.new(start_state, accept_states, rulebook)
end
def accepts?(string)
to_dfa.tap { |dfa| dfa.read_string(string) }.accepting?
end
end
Now, using the automata below as a example, we are going to construct it using our Ruby objects:
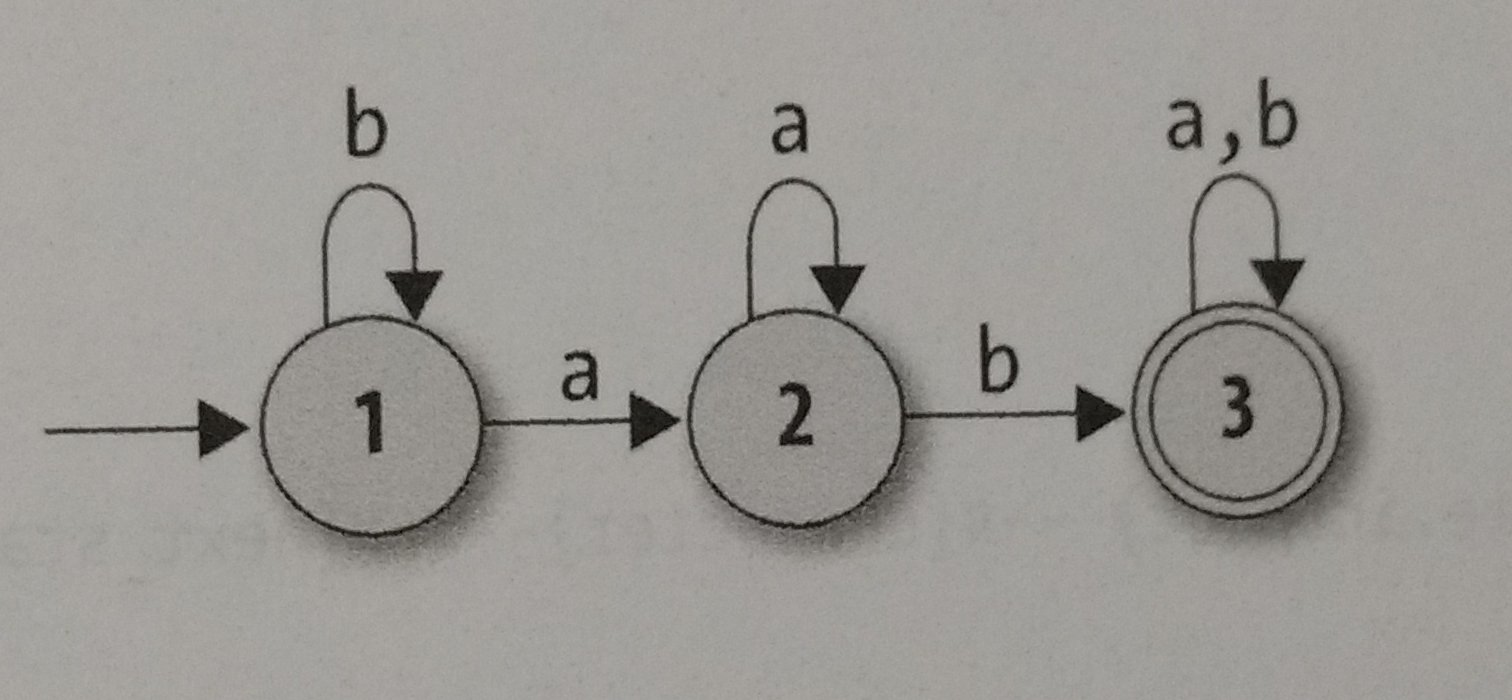
rulebook = DFARulebook.new ([
FARule.new(1, 'a', 2), FARule.new(2, 'a', 2),
FARule.new(3, 'a', 3), FARule.new(1, 'b', 1),
FARule.new(2, 'b', 3), FARule.new(3, 'b', 3)
])
=> #<struct DFARulebook ...>
rulebook.next_state(1, 'a')
=> 2
dfa = DFA.new(1, [3], rulebook); dfa.accepting?
=> false #since the current state is 1 and the accept state is only 3.
dfa.read_character('b'); dfa.accepting?
=> false
dfa.read_string('baaab'); dfa.accepting?
=> true
dfa_design = DFADesign.new(1, [3], rulebook)
=> #<struct DFADesign ...>
dfa_design.accepts?('a')
=> false
dfa_design.accepts?('baba')
=> true
DFAs are very simple and we are already familiar with them. Now that we have already tried the deterministic way of implementing an automata, we can try to implement an automata with contradictions and omissions, with rules that can follow two or more paths. This type of automata is called NFA(Non-Deterministic Finite Automaton).
Since we can have multiple different paths with only one character, we won’t have just one current state, but a collection of them. For example, if I’m on state 1, and the automata reads a ‘b’, I can stay on state 1 or go to state 2, this is how NFA works. So, it seems to be difficult to implement this type of automata on Ruby, we will need to thing on the possibilities. We could do the implementation recursively trying all the possibilities, or even simulate all possibilities in parallel by spawning new threads every time the machine has more than one rule it can follow. Those implementation looks nice, but, they are too complicated to be implemented, but fortunately, we have an easier way to simulate an NFA. just as DFAs, we can keep track of the current state, in NFAs simulation, we can keep track of the possibilities of states. Let’s start implementing the NFA rulebook:
require "set"
class NFARulebook < Struct.new(:rules)
def next_states(states, character)
states.flat_map { |state| follow_rules_for(state, character) }.to_set
end
def follow_rules_for(state, character)
rules_for(state, character).map(&:follow)
end
def rules_for(state, character)
rules.select { |rule| rule.applies_to?(state, character) }
end
end
We are using the Set class from Ruby to avoid duplication: [1, 1, 2, 2] = Set[1, 2], to ignore orders: [2, 1] = Set[1, 2], and provide us 3 operations: intersection(#&), union(#+) and subset(#subset?). Now we can create the NFA object:
class NFA < Struct.new(:current_states, :accept_states, :rulebook)
def accepting?
(current_states & accept_states).any?
end
def read_character(character)
self.current_states = rulebook.next_states(current_states, character)
end
def read_string(string)
string.chars.each do |character|
read_character(character)
end
end
end
The NFA class is very similar to the DFA class, the only difference is that we have a set of possible current states instead of a single definite current state. Now let’s implement an NFADesign object to automatically manufacture new NFA instances for us:
class NFADesign < Struct.new(:start_state, :accept_states, :rulebook)
def accepts?(string)
to_nfa.tap { |nfa| nfa.read_string(string) }.accepting?
end
def to_nfa
NFA.new(current_states, accept_states, rulebook)
end
end
Now, let’s use the NFA below to use our objects:
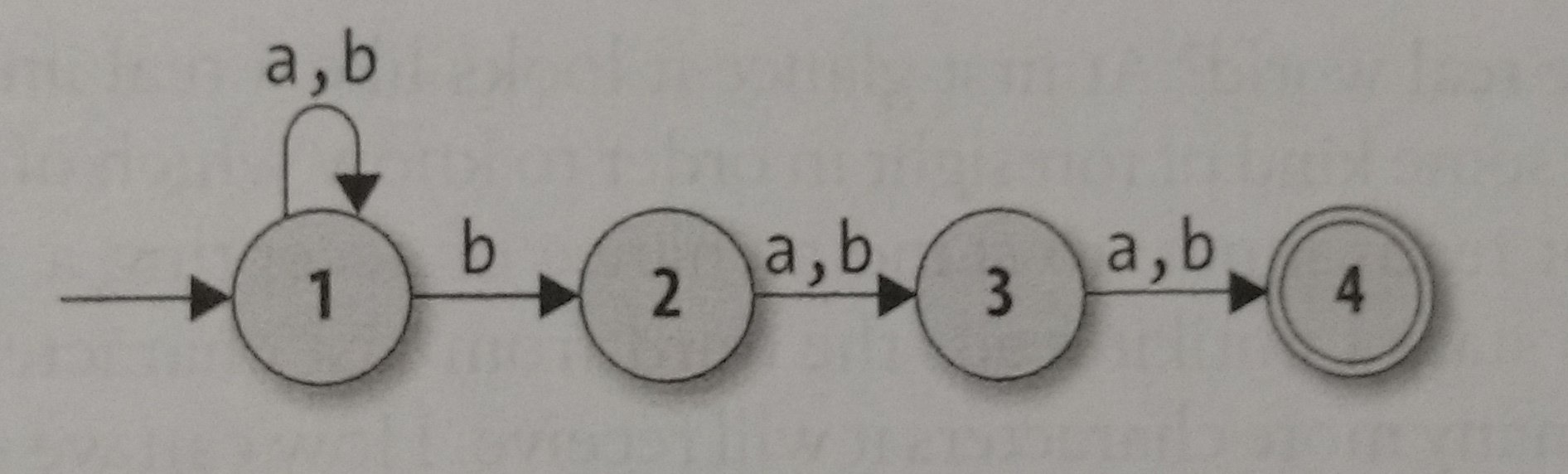
rulebook = NFARulebook.new([
FARule.new(1, 'a', 1), FARule.new(2, 'a', 3),
FARule.new(3, 'a', 4), FARule.new(1, 'b', 1),
FARule.new(1, 'b', 2), FARule.new(2, 'b', 3),
FARule.new(3, 'b', 4)
])
=> #<struct NFARulebook ...>
rulebook.next_states(Set[1], 'b')
=> #<Set: {1, 2}>
rulebook.next_states(Set[1, 2], 'a')
=> #<Set: {1, 3}>
nfa = NFA.new(Set[1], [4], rulebook); nfa.accepting?
=> false
nfa.read_character('b'); nfa.accepting?
=> false
nfa = NFA.new(Set[1], [4], rulebook); nfa.accepting?
=> false
nfa.read_string('bbbbb');nfa.accepting?
=> true
nfa_design = NFADesign.new(1, [4], rulebook)
=> #<Struct NFADesign ...>
nfa_design.accepts?('bab')
=> true
nfa_design.accepts?('bbbbb')
=> true
Let’s solve a situation: I need an automata that accepts string with amounts of a’s multiple of two or three, how would it look like? like this one below?
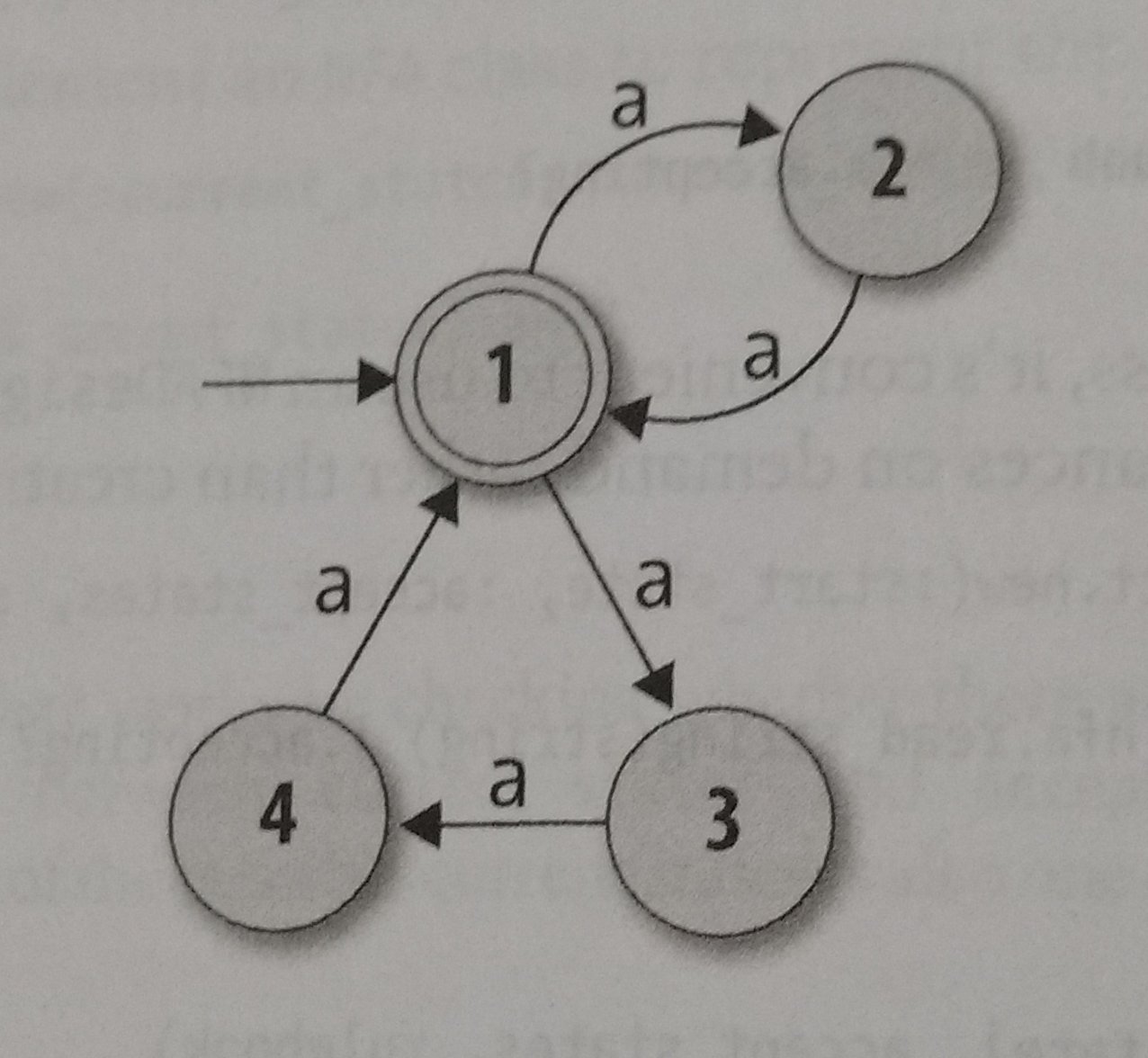
This one looks nice, but… It accepts ‘aaaaa’, and 5 isn’t multiple of two or three… So, what is the solution? There is one thing in NFA called ‘Free Moves’. Free moves are paths that don’t need any input to be used. The solution for this situation would look like this with free moves:
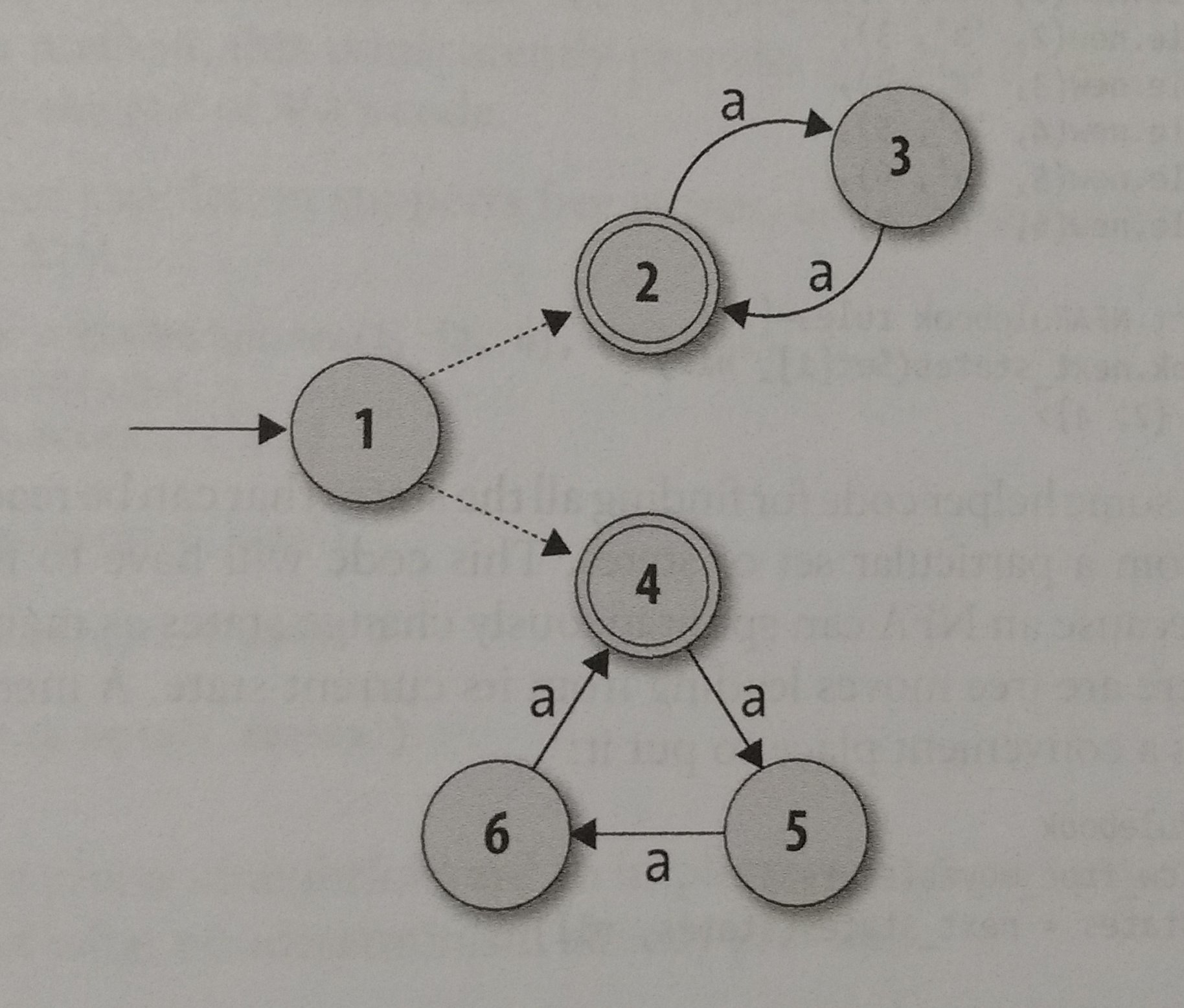
Those dotted arrows are the free moves. In this case, if we are in state 1, our possibles next states are 2 and 4, regardless of input. Now, let’s try to implement free moves in Ruby, First, we need a way to represent free moves, I think the best way is a FARule with the character value equals to nil. Then, on the rulebook we would need to implement a new method that would help us to find more and more states:
Class NFARulebook
def follow_free_moves(states)
more_states = next_states(states, nil)
if more_states.subset?(states)
states
else
follow_free_moves(states + more_states)
end
end
end
Then, we will need to make #current_states from NFA follow the free moves:
Class NFA
def current_states
rulebook.follow_free_moves(super)
end
end
Now, let’s test the free moves:
rulebook = NFARulebook.new([
FARule.new(1, nil, 2), FARule.new(2, 'a', 3),
FARule.new(3, 'a', 2), FARule.new(4, 'a', 5),
FARule.new(5, 'a', 6), FARule.new(6, 'a', 4), FARule.new(1, nil, 4)
])
=> #<struct NFARulebook ...>
rulebook.follow_free_moves(Set[1])
=> #<Set: {2, 4}>
nfa_design = NFADesign.new(1, [2, 4], rulebook)
=> #<struct NFADesign ...>
nfa_design.accepts?('aa')
=> true
nfa_design.accepts?('aaa')
=> true
nfa_design.accepts?('aaaaa')
=> false
nfa_design.accepts?('aaaaaa')
=> true
Now, let’s try to use those automatas to implement a little bit of Regular Expressions. But first, what is a Regular Expression? Regular expression provide a language for writing textual patterns against which strings may be matched. Some examples of RegExp:
- hello -> matches ‘hello’
-
hello goodbye -> matches ‘hello’ and ‘goodbye’ - (hello)* -> matches ‘hello’, ‘hellohello’, ‘hellohellohello’, and so on, as well as the empty string
So, before implementing it, let’s discuss about the syntax we are going to use:
- An empty regular expression, matches the empty string or nothing.
- A regular containing a single character, matches a string containing this character.
- Concatenate two regular expressions, matches the string that matches each expression, concatenated.
- Choose between two expressions, matches one expression and the other one.
- Repeat a pattern zero or more times, matches the string with the character of the expression repeated 0 or more times.
Having the syntax in mind, let’s implement the Regular Expression syntax:
module Pattern
def bracket(outer_precedence)
if precedence < outer_precedence
'(' + to_s + ')'
else
to_s
end
end
def inspect
"/#{self}/"
end
end
class Empty
include Pattern
def to_s
''
end
def precedence
3
end
end
class Literal < Struct.new(:character)
include Pattern
def to_s
character
end
def precedence
3
end
end
class Concatenate < Struct.new(:first, :second)
include Pattern
def to_s
[first, second].map { |pattern| pattern.bracket(precedence) }.join
end
def precedence
1
end
end
class Choose < Struct.new(:first, :second)
include Pattern
def to_s
[first, second].map { |pattern| pattern.bracket(precedence) }.join('|')
end
def precedence
0
end
end
class Repeat < Struct.new(:pattern)
include Pattern
def to_s
pattern.bracket(precedence) + '*'
end
def precedence
2
end
end
Let’s see how it looks like:
pattern =
Repeat.new(
Choose.new(
Concatenate.new(Literal.new('a'), Literal.new('b')),
Literal.new('a')
)
)
=> /(ab|a)*/
Let’s start to think about the semantics. Let’s start with Empty, that it’s just a one-state NFA, easy, no?
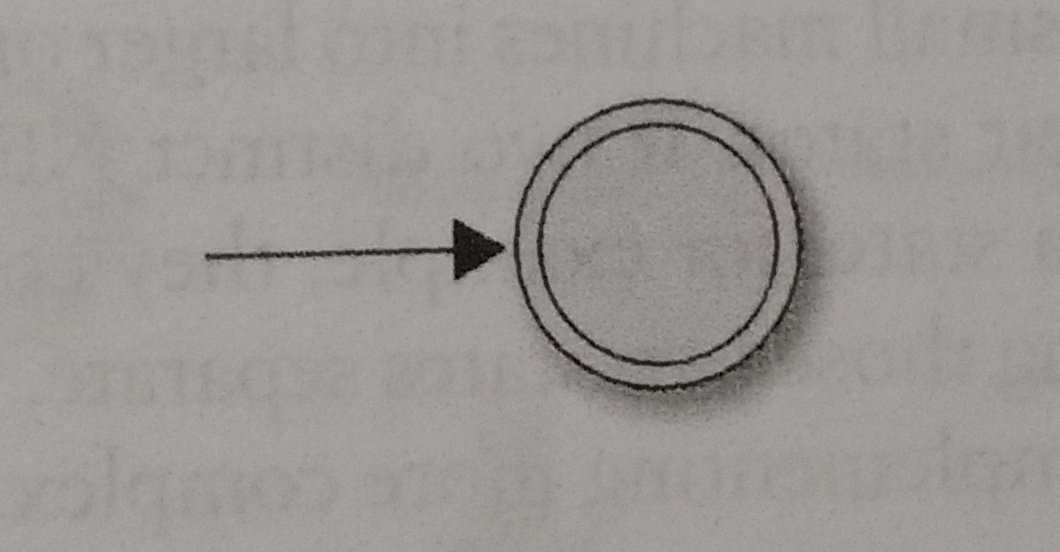
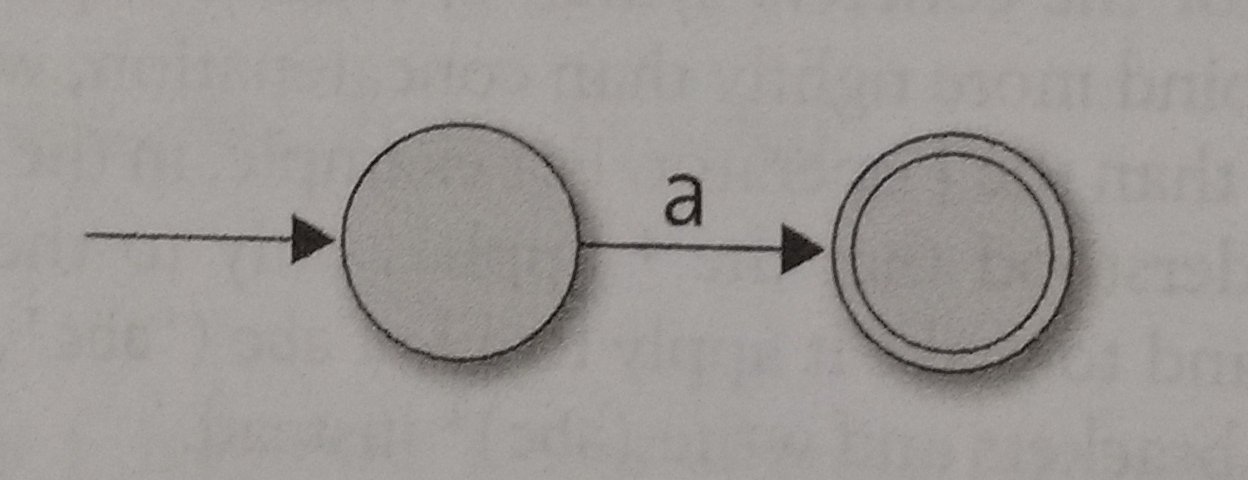
Similary, the literal, single-character pattern into NFA that only accepts the single-character containing that character.
Class Empty
def to_nfa_design
start_state = Object.new
accept_states = [start_state ]
rulebook = NFARulebook.new([])
NFADesign.new(start_state, accept_states, rulebook)
end
end
Class Literal
def to_nfa_design
start_state = Object.new
accept_states = Object.new
rule = FARule.new(start_state, character, accept_states)
rulebook = NFARulebook.new([rule])
NFADesign.new(start_state, [accept_states], rulebook)
end
end
Instead of using the NFADesign to see if the NFA accepts a string, let’s implement a method called “matches?” on the Pattern module.
module Pattern
def matches?(string)
to_nfa_design.accepts?(string)
end
end
Now, let’s try to do Concatenate, Choose and Repeat. Let’s begin with Concatenate. We know how to turn an expression into an NFA, for example, the expression a and b, how do we turn ab into one?
We coud connect them with a free move, keeping the start state of the first expression and the accept state of the second expression, like this:
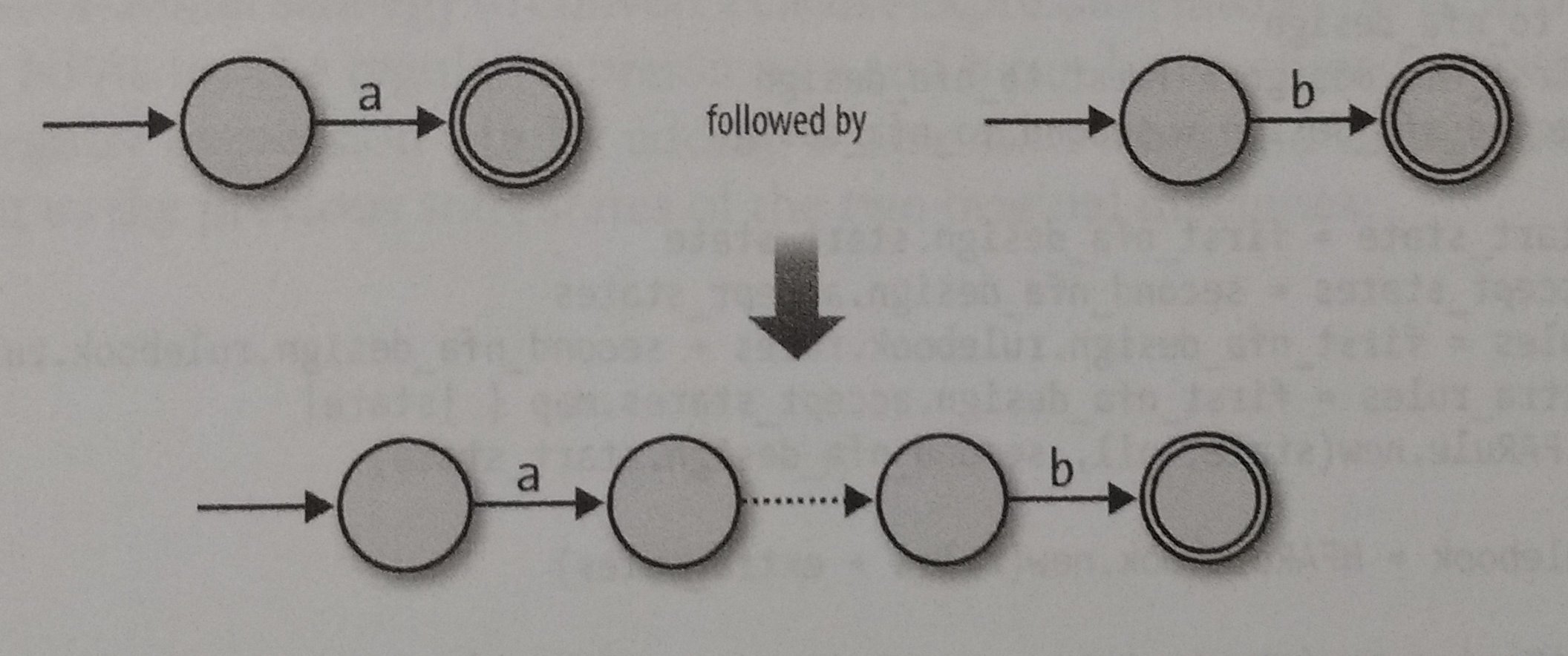
So, the ingredients to implement Concatenate are:
- Start state of the first NFA.
- Accept state of the second NFA.
- All rules.
- Some extra free moves to connect each of the first NFA’s old accept states to the second NFA’s old start state.
Now, let’s implement it:
class Concatenate
def to_nfa_design
first_nfa_design = first.to_nfa_design
second_nfa_design = second.to_nfa_design
start_state = first_nfa_design.start_state
accept_states = second_nfa_design.accept_states
rules = first_nfa_design.rulebook.rules + second_nfa_design.rulebook.rules
extra_rules = first_nfa_design.accept_states.map {
|state| FARule.new(state, nil, second_nfa_design.start_state)
}
rulebook = NFARulebook.new(rules + extra_rules)
NFADesign.new(start_state, accept_states, rulebook)
end
end
We can use a similar strategy to Choose, but this time, we are going to use two free moves to connect the start state to both start states, like this:
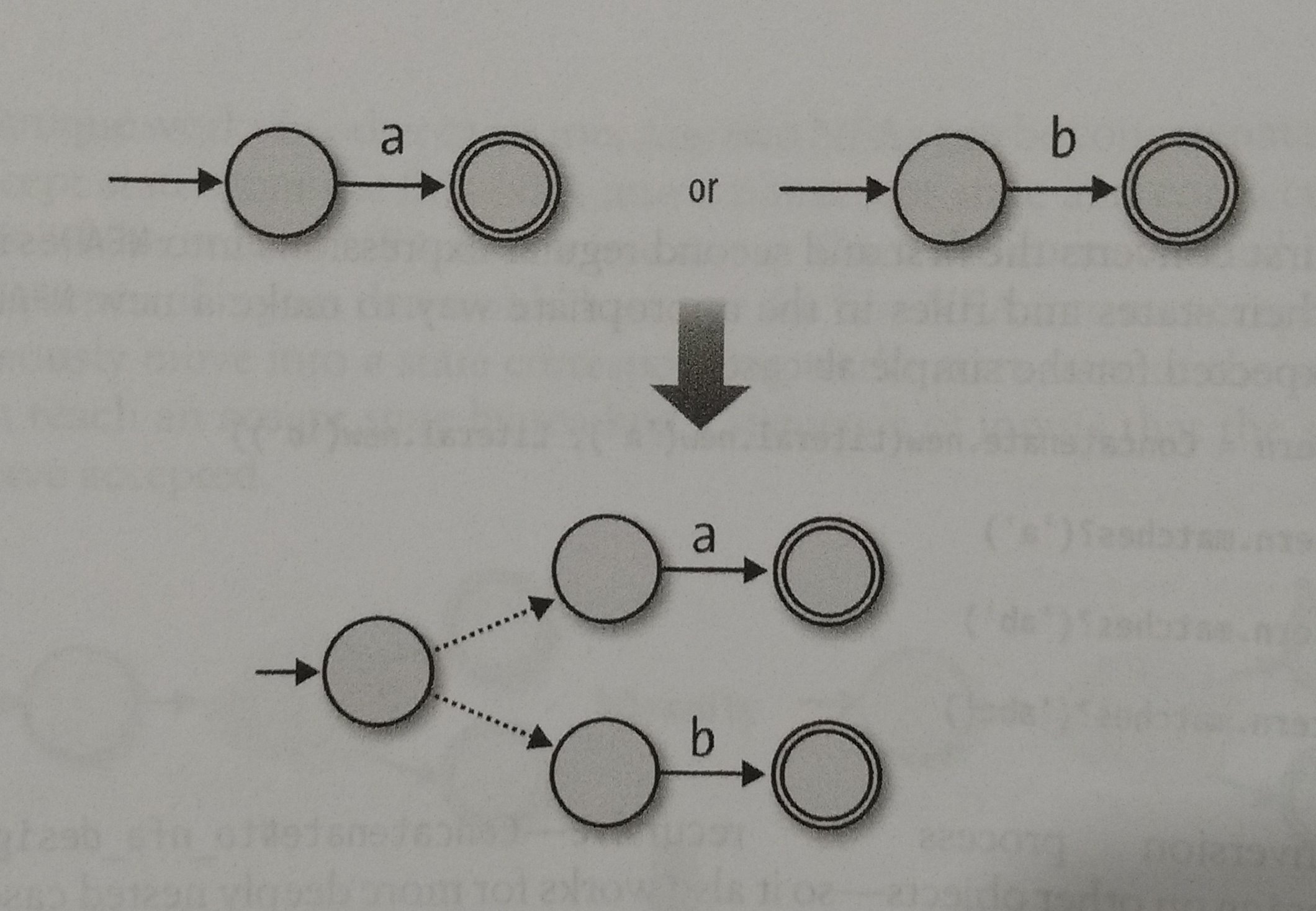
So, the ingredients to implement Choose are:
- A new start state.
- Both accept states.
- All rules.
- Two extra free moves to connect new start state with each of the NFA’s old start states.
Having the ingredients in mind, let’s implement it:
class Choose
def to_nfa_design
first_nfa_design = first.to_nfa_design
second_nfa_design = second.to_nfa_design
start_state = Object.new
accept_states = first_nfa_design.accept_states + second_nfa_design.accept_states
rules = first_nfa_design.rulebook.rules + second_nfa_design.rulebook.rules
extra_rules = [first_nfa_design, second_nfa_design].map {
|nfa_design| FARule.new(start_state, nil, nfa_design.start_state)
}
rulebook = NFARulebook.new(rules + extra_rules)
NFADesign.new(start_state, accept_states, rulebook)
end
end
And finally, the Repeat object, we can build it making additions of two things: Adding a free move from its accept state to its start state, so it can match more than one repetition, and add a new accepting start state with a free move to the old start state, so it can match the empty state, here’s how that looks:
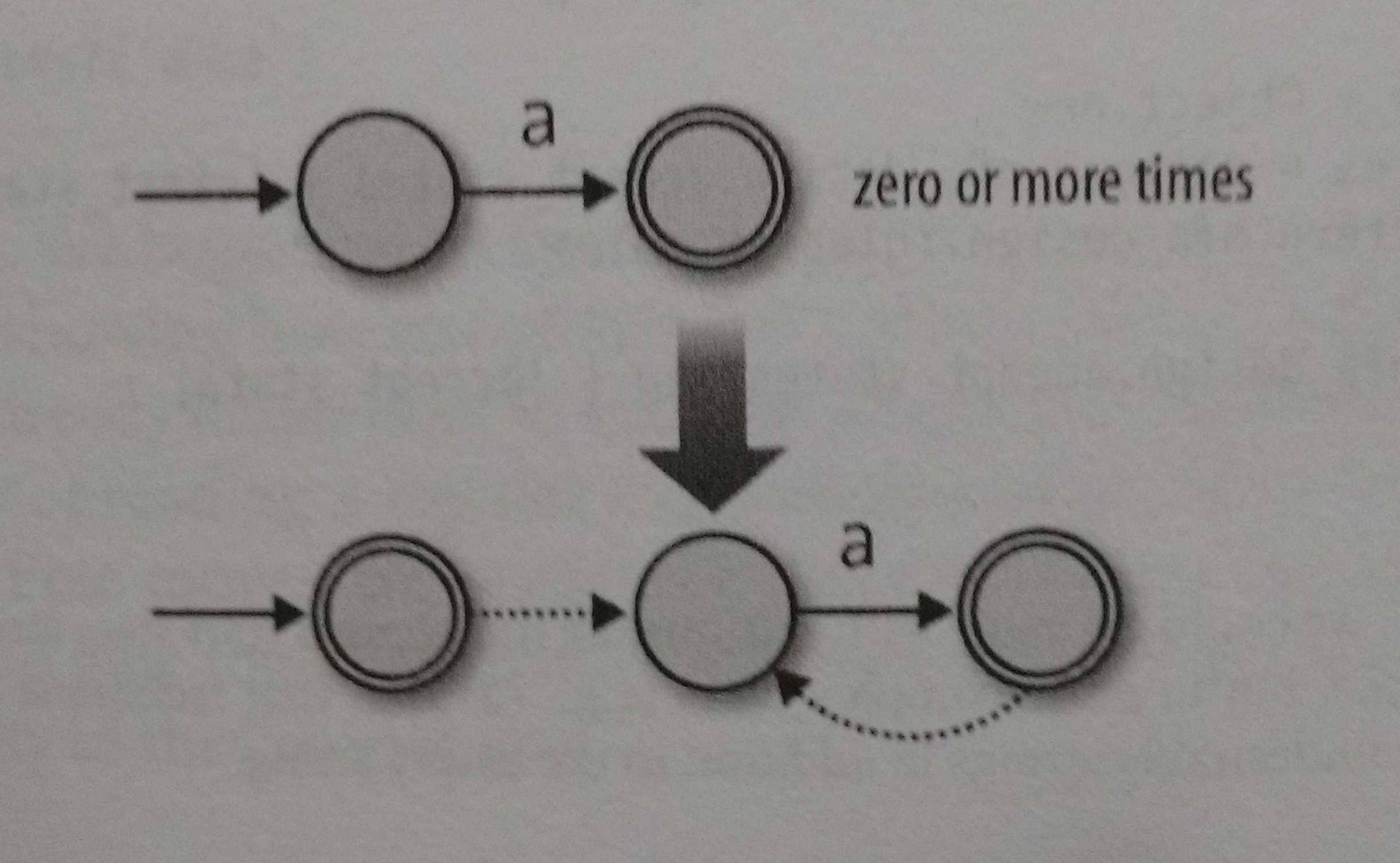
This time we will need:
- A new start state
- All the accept states from the old NFA
- All rules
- Some extra free moves to connect each of the old NFA’s accept states to its old start state
- Another free move to connect the new start with the old one.
Let’s turn that into code:
class Repeat
def to_nfa_design
pattern_nfa_design = pattern.to_nfa_design
start_state = Object.new
accept_states = pattern_nfa_design.accept_states + [start_state]
rules = pattern_nfa_design.rulebook.rules
extra_rules = pattern_nfa_design.accept_states.map {
|accept_state| FARule.new(accept_state, nil, pattern_nfa_design.start_state)
} + [FARule.new(start_state, nil, pattern_nfa_design.start_state)]
rulebook = NFARulebook.new(rules + extra_rules)
NFADesign.new(start_state, accept_states, rulebook)
end
end
If you have any doubts about this post, talk with me on Facebook or Twitter