Understanding how computation works part 2-2

On this post, I will try to make you understand more about computer science. So, in this part of the post we are going to parse the RegExp implementation and we will convert a NFA into a DFA.
Now, we can parse the RegExp implementation with Treetop, as we did on the previous post. let’s do it:
grammar Pattern
rule choose
first:concatenate_or_empty '|' rest:choose {
def to_ast
Choose.new(first.to_ast, rest.to_ast)
end
}
/
concatenate
end
rule concatenate_or_empty
concatenate / empty
end
rule concatenate
first:repeat rest:concatenate {
def to_ast
Concatenate.new(first.to_ast, rest.to_ast)
end
}
/
repeat
end
rule empty
'' {
def to_ast
Empty.new
end
}
end
rule repeat
brackets '' {
def to_ast
Repeat.new(brackets.to_ast)
end
}
/
brackets
end
rule brackets
'(' choose ')' {
def to_ast
choose.to_ast
end
}
/
literal
end
rule literal
[a-z] {
def to_ast
Literal.new(text_value)
end
}
end
end
Using parser, let’s test a more complex expression:
require "treetop"
=> true
Treetop.load('pattern')
=> PatternParser
parse_tree = PatternParser.new.parse('(a(|b))*')
=> 'big output'
pattern = parse_tree.to_ast
=> /(a(|b))*/
pattern.matches?('abaab')
=> true
pattern.matches?('abba')
=> false
After learning what is a DFA and a NFA, and even implementing a RegExp using NFA, we can conclude that any NFA can do more than a DFA, NFA is just a different way of writing an automata, the only difference between those two is that NFAs have free moves and don’t need to follow the deterministic constraints. So, it is evident that we can convert a NFA into a DFA, right? Yeah, and that is what we are going to do right now. Let’s try to convert this NFA into a DFA:
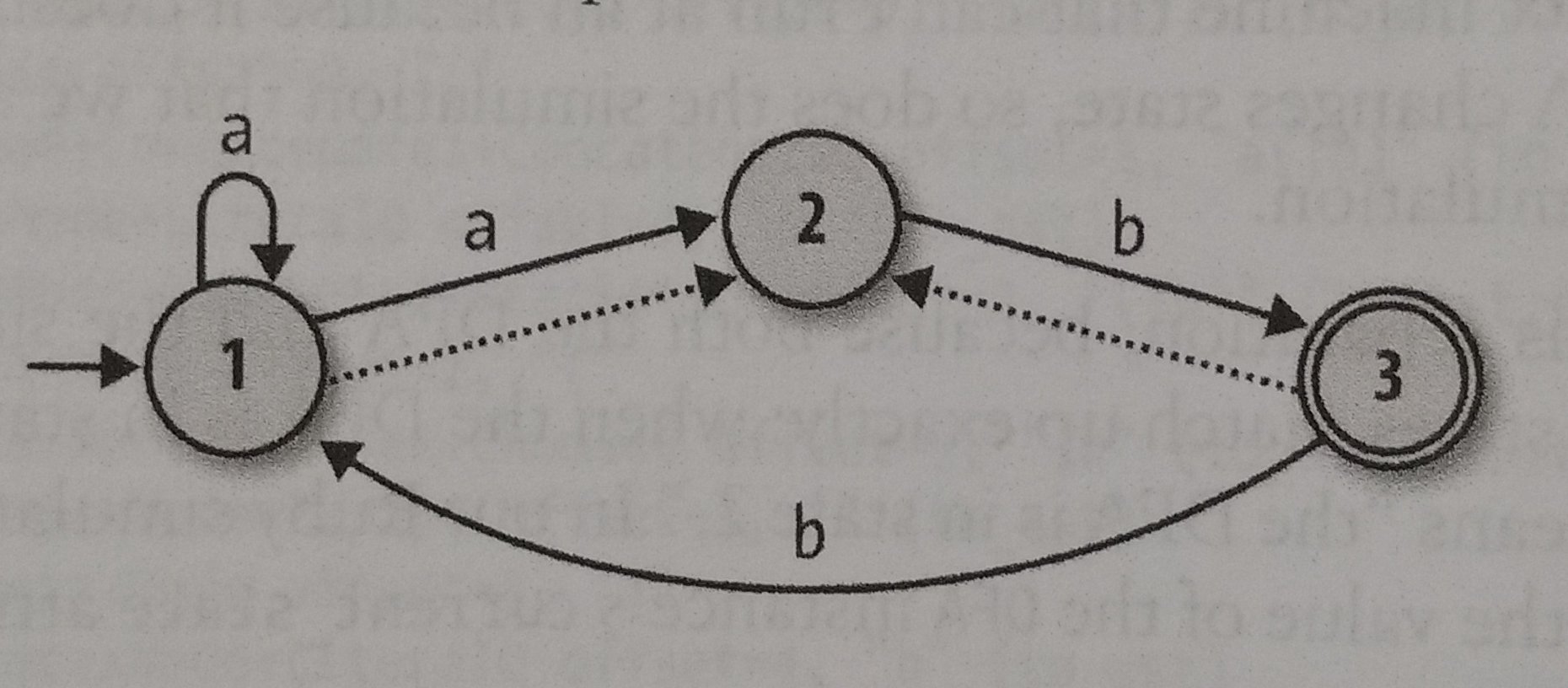
Let’s think about it behavior:
- It is possible for this NFA to be in state 1 or 2 before reading any input. So we can begin on a state called 1 or 2.
- If it reads an ‘a’, it will remain on the state 1 or 2, since in the NFA it can remain on the state 1 or go to the state 2.
- If it reads a ‘b’, it is possible to be on state 2 or 3, state 2 thanks to the free move, and 3 thanks to the free move too, but it can goes to the state 3 after using the free move.
With this behaviors, we could create a DFA like this:
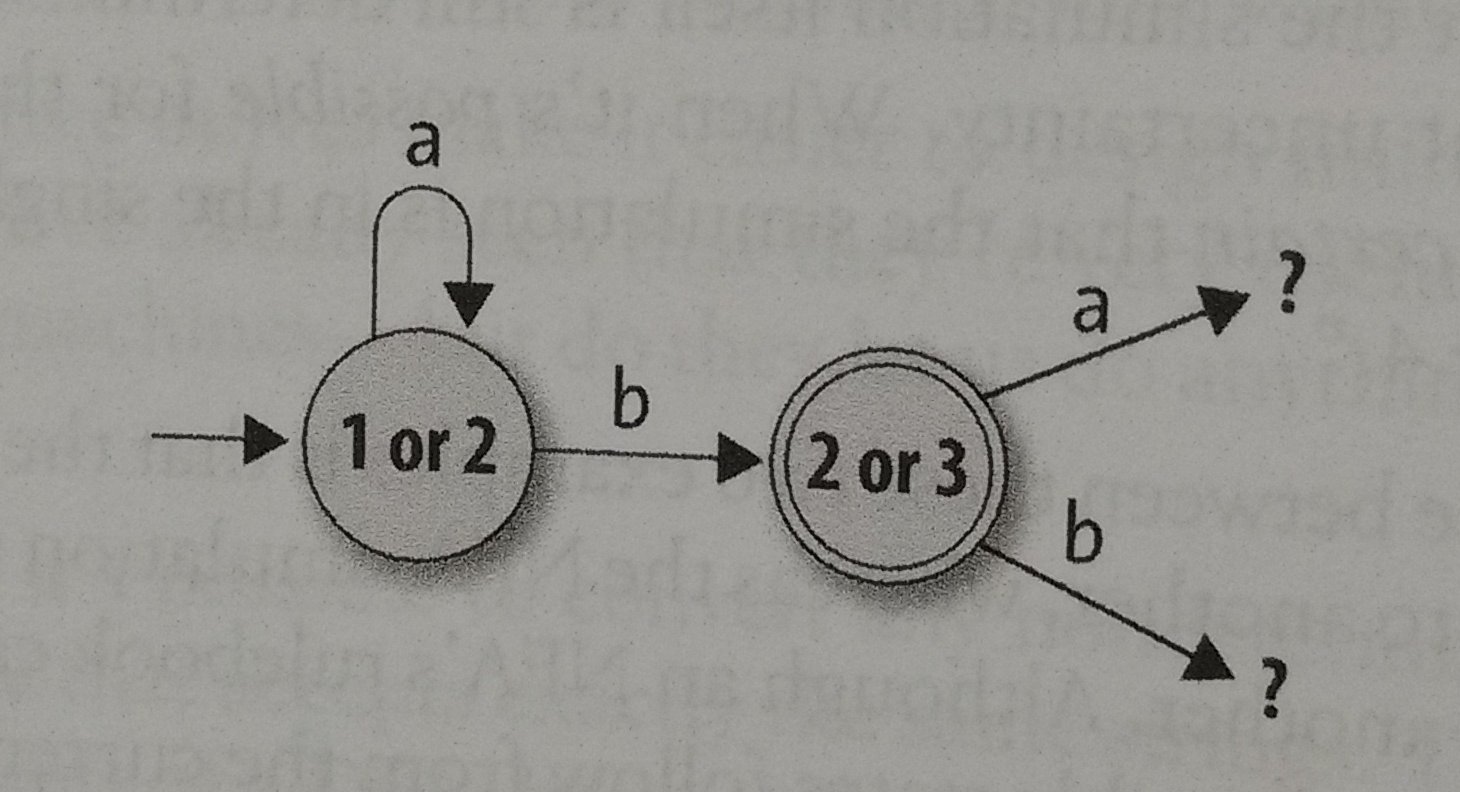
So, it seems a little bit incomplete, so we will need to do a list with each possible movement and then create a better DFA. After making this list, we can come out with something like this:
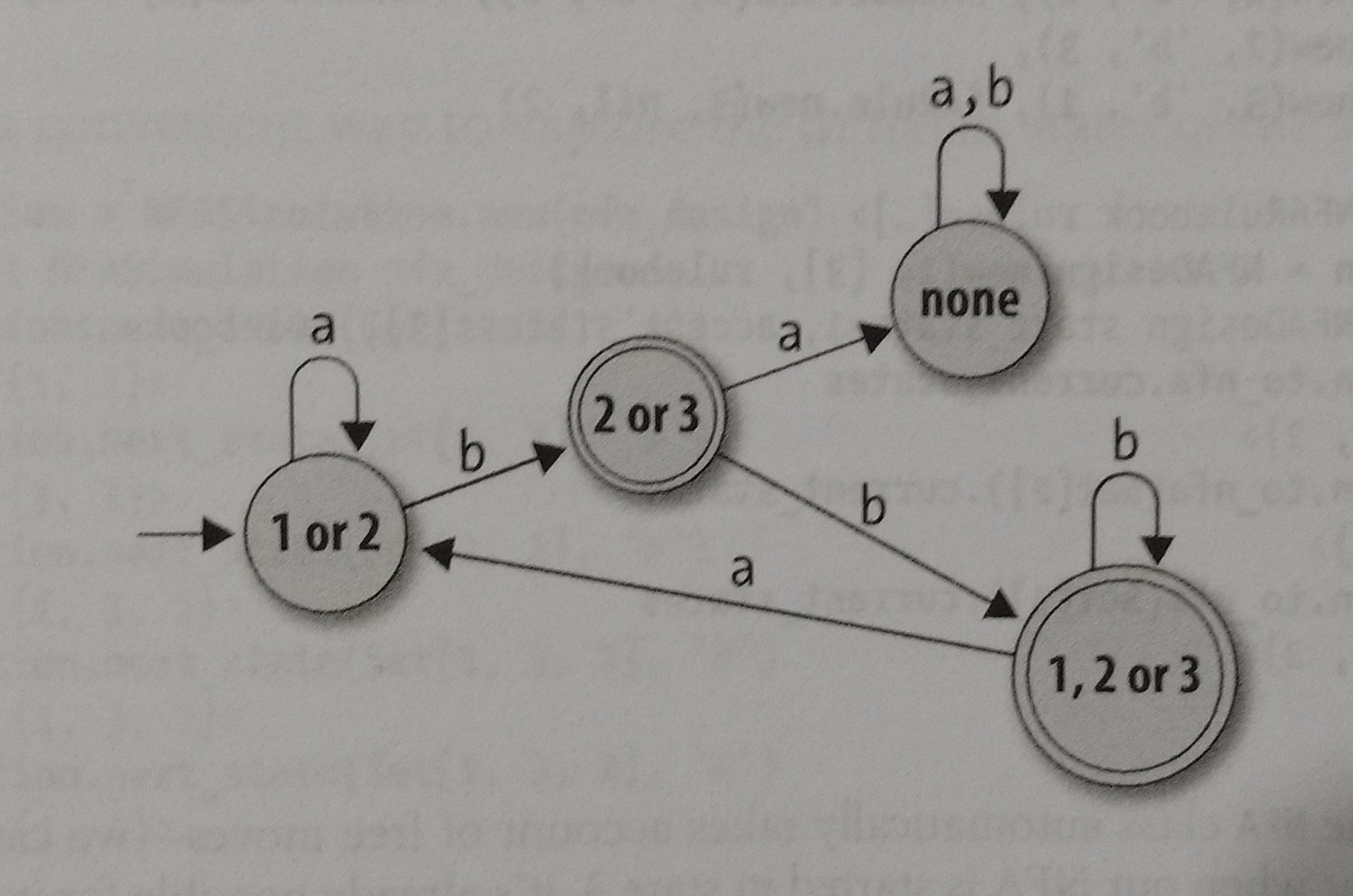
And now we have a better DFA, and we can implement a NFA_to_DFA conversion in Ruby. We can do it creating a new class called NFASimulation that collects the informations of the NFA and then it can assemble those informations into a DFA. Let’s do one thing before starting, let’s allow our NFADesign to determine a current_state, not only use the start_state.
class NFADesign
def to_nfa(current_states = Set[start_state])
NFA.new(current_states, accept_states, rulebook)
end
end
Let’s start the implementation of NFASimulation with a method called “next_state” that will simulate a state and will take a character, and will get the new state back by inspecting the NFA:
class NFASimulation < Struct.new(:nfa_design)
def next_state(state, character)
nfa_design.to_nfa(state).tap {
|nfa| nfa.read_character(character)
}.current_states
end
end
Now we can simulate a movement just by using this method:
rulebook = NFARulebook.new([
FARule.new(1, 'a', 1),
FARule.new(1, 'a', 2),
FARule.new(1, nil, 2),
FARule.new(2, 'b', 3),
FARule.new(3, 'b', 1),
FARule.new(3, nil, 2)
])
=> #<struct NFARulebook rules=[..]>
nfa_design = NFADesign.new(1, [3], rulebook)
=> #<struct NFADesign ..>
simulation = NFASimulation.new(nfa_design)
=> #<struct NFASimulation ..>
simulation.next_state(Set[1, 2], 'a')
=> #<Set: {1,2}>
simulation.next_state(Set[1, 2], 'b')
=> #<Set {2,3}>
Now we need a method to tell us what characters the NFA can read, let’s implement this method on NFARulebook, and we need to use this method on NFASimulation called “rules_for”, but this time, rules_for will return the rules for a particular Set of states, let’s do it:
class NFARulebook
def alphabet
rules.map(&:character).compact.uniq
end
end
class NFASimulation
def rules_for(state)
nfa_design.rulebook.alphabet.map { |character|
FARule.new(state, character, next_state(state, character))
}
end
end
Let’s see how they work:
rulebook.alphabet
=> ['a', 'b']
simulation.rules_for(Set[1,2])
=> [
#<FARule #<Set: {1, 2}> --a--> #<Set: {1, 2}>>,
#<FARule #<Set: {1, 2}> --b--> #<Set: {3, 2}>>
]
the #rules_for give us a way to explore the rules and discover new states, and repeating it, we can find all possible states. For this we could implement a method called “discover_states_and_rules”, which recursively finds more states, similar to #follow_free_moves:
class NFASimulation
def discover_states_and_rules(states)
rules = states.flat_map {
|state| rules_for(state)
}
more_states = rules.map(&:follow).to_set
if more_states.subset?(states)
[states, rules]
else
discover_states_and_rules(states + more_states)
end
end
end
And finally, the method that will convert the NFA to DFA:
class NFASimulation
def to_dfa_design
start_state = nfa_design.to_nfa.current_states
states, rules = discover_states_and_rules(Set[start_state])
accept_states = states.select { |state| nfa_design.to_nfa(state).accepting? }
DFADesign.new(start_state, accept_states, DFARulebook.new(rules)) end end </code>
As you can see, we are just taking the informations from the NFA and using them to return a new DFADesign. Let’s test the methods implemented previously and let’s convert a NFA into a DFA:
start_state = nfa_design.to_nfa.current_states
=>#<Set: {1, 2}>
simulation.discover_states_and_rules(Set[start_state])
=> [
#<Set:
{#<Set: {1, 2}>,
#<Set: {3, 2}>,
#<Set: {}>,
#<Set: {1, 3, 2}>}>,
[
#<FARule #<Set: {1, 2}> --a--> #<Set: {1, 2}>>,
#<FARule #<Set: {1, 2}> --b--> #<Set: {3, 2}>>,
#<FARule #<Set: {3, 2}> --a--> #<Set: {}>>,
#<FARule #<Set: {3, 2}> --b--> #<Set: {1, 3, 2}>>,
#<FARule #<Set: {}> --a--> #<Set: {}>>,
#<FARule #<Set: {}> --b--> #<Set: {}>>,
#<FARule #<Set: {1, 3, 2}> --a--> #<Set: {1, 2}>>,
#<FARule #<Set: {1, 3, 2}> --b--> #<Set: {1, 3, 2}>>
]
]
dfa_design = simulation.to_dfa_design
=>#
If you have any doubts about this post, talk with me on Facebook or Twitter